|
清华大学数学实验视频教程全程录像免费下载地址:
链接:https://pan.baidu.com/s/16xYKksQygC11dufVx1Lm8A
提取码:8765
《数学实验》教学大纲
[教学进度]
l 教师每周(3学时)讲授1个实验,布置2-3道实验习题。
l 学生每周完成实验习题(通常要上机完成),提交实验报告;期末上机考试。
[基本要求]
l 了解主要内容的基本原理;
l 知道主要内容的有效算法
l 会用MATLAB(或LINDO/LINGO软件)实现这些有效算法
l 能对计算结果作简单分析
l 简化实际问题的建模、求解和分析
[分实验基本内容和要求]
预备实验:MATLAB使用练习
l 掌握MATLAB的基本使用方法
实验1 数学建模初步
l 通过实例了解数学建模的一般步骤;
l 在以后的数学实验中用数学建模方法解决经过简化的实际问题;
l 自觉培养用数学方法解决实际问题的意识和能力。
实验2 差分方程与数值微分
l 一阶常系数差分方程;
l 高阶常系数差分方程;
l 一阶常系数差分方程组;
l 非线性差分方程;
l 数值微分及其MATLAB实现;
l 用差分方程或数值微分解决简单的实际问题。
实验3 插值与数值积分
l 插值问题提法和求解思路;
l Lagrange插值的原理和优缺点;
l 分段线性和三次样条插值的原理和优缺点;
l 用MATLAB实现分段线性和三次样条插值;
l 梯形、辛普森积分公式的原理及MATLAB实现
l 数值积分公式的误差——收敛阶的概念
l 高斯积分公式
l 广义积分与多重积分
l 用插值和数值积分解决简单的实际问题。
实验4 常微分方程数值解
l 欧拉方法的原理及龙格-库塔方法的思路
l 局部截断误差和精度的概念
l 龙格-库塔方法的MATLAB实现,包括求解微分方程组和高阶微分方程
l 用微分方程解决简单的实际问题。
实验5 线性方程组的解法
l 主元素消去法和LU分解的原理
l 方程组病态、向量和矩阵范数、条件数的概念
l 迭代法的原理以及收敛的概念和条件
l 用MATLAB解方程组,稀疏矩阵的处理
l 拟合问题提法及最小二乘法的原理和结果;
l 用线性方程组及最小二乘法解简单的实际问题。
实验6 非线性方程近似解
l 迭代法原理及收敛、收敛阶的概念
l 用牛顿法解非线性方程和方程组
l 非线性迭代法与混沌现象
l 用非线性方程解简单的实际问题。
实验7 无约束优化
l 无约束优化模型及最优解的必要条件
l 最速下降法、牛顿法、拟牛顿法的原理
l 非线性最小二乘的解法
l MATLAB优化工具箱的用法,包括控制参数的功能,算法选择等
l 用无约束优化(包括非线性最小二乘拟合)解决简单的实际问题。
实验8 约束优化
l 线性规划模型、解的性质和求解思路
l 用MATLAB解线性规划,拉格朗日乘子的用途
l 非线性规划模型、最优解的必要条件
l 用MATLAB解非线性规划,包括控制参数的功能
l 用线性规划和非线性规划解决简单的实际问题
实验9 整数规划
l 整数规划模型、解的性质、松弛问题
l 解整数规划的分枝定界法和动态规划法
l 用LINDO解线性整数规划
l 用LINGO解非线性整数规划
l 用整数规划解决简单的实际问题
实验10数据的统计描述和分析
l 样本、频数、直方图、统计量(样本均值、标准差)的概念
l 正态, t, c2, F分布的由来,用MATLAB计算这些分布(密度、逆分布)
l 正态总体下样本统计量的分布
l 蒙特卡罗方法的原理及MATLAB实现
l 用概率统计的基本思想解决简单的实际问题
实验11 统计推断
l 参数估计、置信区间、置信水平
l 假设检验的思路,一总体和两总体均值的检验,双边和单边检验
l 用MATLAB实现参数估计和假设检验
l 实际问题的参数估计和假设检验
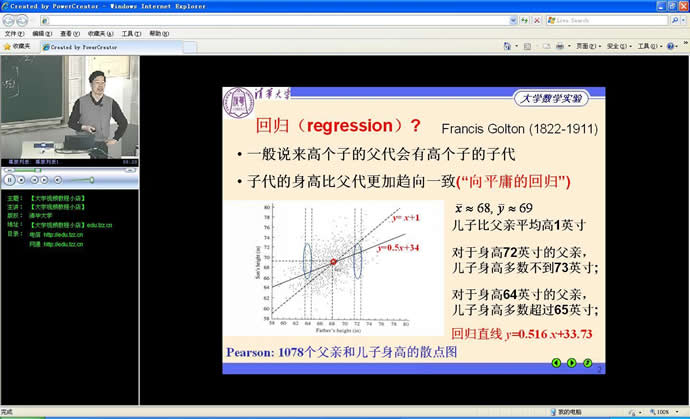
实验12 回归分析
l 回归分析要解决的问题(与数据拟合的关系)
l 多元线性回归模型和系数的检验, 及MATLAB实现
l 一元多项式、多元二项式回归, 逐步回归,非线性回归,及MATLAB实现
l 用回归分析解决简单的实际问题
实验13 数学建模综合
l 综合应用各种方法,对实际问题建模、求解和分析
教学内容
l 教学内容的设计思想
数学实验是清华大学在数学教学体系和内容改革中为非数学类专业创立的新课,是4门数学主干课程的最后一门(前3门是微积分、代数与几何、随机数学方法),起着承上(上述3门数学基础课)、启下(后续课、研究生课程及数学的应用)的作用,其对象主要是本科二年级学生。
数学实验课的宗旨是,在教师指导下以学生在计算机上自己动手、动眼、动脑为主,通过用数学软件做实验,学习解决实际问题常用的数学方法,并在此基础上分析、解决经过简化的实际问题,提高学数学、用数学的兴趣、意识和能力,促成数学教学的良性循环。
l 教学内容的体系结构
数学实验是一门重组课程,它集数值计算、优化方法、数理统计、数学建模以及计算机技术于一体,以“应用数学基本原理、了解主要数值算法、借助数学软件实现、培养数学建模能力”为基本要求。
力求做到既保证本科生学到比较广泛且相当有用的数学知识,以及初步的分析、解决实际问题的思路与方法,又为那些要求掌握更深入的数学理论和方法的学生,提供许多实际背景,并刺激他们再学习的愿望。
这样做还特别有利于不少院校实行的“本硕贯通”,数学实验课既为研究生的数学课(如数值分析、数学规划、高等数值分析、高等统计等)做了基本知识和实际背景的铺垫,又与这些课程在内容和要求上有较大的区别,形成明显的阶梯。
l 内容设计的基本原则
1. 介绍一些最常用的解决实际问题的数学方法,包括数值计算、优化方法、数理统计的基本原理和算法,一般不讲证明,基本不做笔头练习;
2. 选择一个合适的数学软件平台,如MATLAB,基本上能够方便地实现上述内容的主要算法;
3. 用数学建模为线索贯穿整个课程,从建模初步练习开始,以建模综合练习结束,对上述每一部分内容也尽量从实际问题引入,并落实于这些问题的解决;
4. 最主要的是精心安排学生的实验,每个实验的内容除了为掌握数学方法设计的纯计算题目外,要有足够的(经过简化的)实际题目。
l 课程的具体内容
预备实验(MATLAB使用练习);
实验1 数学建模初步;
实验2 差分方程与数值微分;
实验3 插值与数值积分;
实验4 常微分方程数值解;
实验5 线性方程组的数值解法;
实验6 非线性方程求解;
实验7 无约束优化;
实验8 约束优化;
实验9 整数规划;
实验10 数据的统计与分析;
实验11 统计推断(参数估计和假设检验);
实验12 回归分析;
实验13 数学建模综合。
课程发展的主要历史沿革
数学实验是20世纪末出现在我国大学里的一门新课,开设这门课程的背景是:
1)计算机技术飞速发展的促进
数学在它产生和发展过程中,一直是和人们的实际需要密切相关的,历史上许多科学技术的重大发明都离不开数学,电子计算机的出现也应归功于数学家的奠基性工作。反过来,科学技术和生产活动的进步,又促进了数学的发展。特别是计算机技术的飞速进步为古老的数学提供了威力巨大的工具,彻底改变了长期以来仅靠一张纸、一支笔做数学的传统,使数学的应用在广度和深度上都达到了前所未有的程度,促成了从数学科学到数学技术的转化,成为当今高科技的一个重要组成部分。同时也把数学从数学家的书斋里和课本中解放出来,成为各行各业认识自然、改造社会的有力武器。
教育必须跟踪、反映并预见社会发展的需要,大学的数学教育更应如此。随着计算机强大的运算功能、图形功能的开发和应用方便的数学软件的不断升级,使学生不仅能在很短时间内自由地选择软件、比较算法、分析结果,而且能在屏幕上通过数值的、几何的观察、联想、类比,去发现解决问题的线索,探讨规律性的结果。开设数学实验课正是要充分利用计算机技术提供的有利条件,加强学生自己动手和独立思考的能力。
2)数学教学体系和内容改革的需要
对于非数学类专业的学生,数学主要是分析、解决实际问题的工具,在学生通常学的微积分、线性代数等基础课与用数学手段解决实际问题之间,尚存在着一定的“间隙”。学习以数值计算、优化方法、数理统计和数学建模为主要内容的数学实验课程,既是数学基础课程的巩固和提高,又为基本数学知识和数学的应用之间架起一座桥梁。
内容枯燥、负担沉重、学习积极性不高,一直困扰着大学数学教育,与此形成鲜明对照的是受大环境支配的计算机热。让学生自己动手,用他们喜欢和熟悉的计算机解决一些简化的实际问题,亲身感受其中的酸甜苦辣,“做然后知不足”,从而激发他们进一步学习数学和其他理论课程的兴趣,可以起到促进数学教学良性循环的作用。
目前不少院校正在开展“本硕贯通”的教育改革,本科阶段的“数学实验”课只介绍相关数学工具的基本原理、方法、软件实现及其应用,这就为要求掌握更深入的数学理论和方法的研究生阶段的数学课程提供了许多实际背景,刺激了学生再学习的愿望。
3)数学建模课程和数学建模竞赛的启示
二十年前进入大学课堂的数学建模课程,对培养学生利用数学工具分析和解决实际问题的能力及数学教学改革起了显著的促进作用,但是限于当时数学软件的发展和使用水平,数学建模课往往是纸上谈兵,学生少有机会自己动手,借助计算机去求解已经建立了模型的实际问题。目前正蓬勃开展的全国大学生数学建模竞赛,可以说是数学建模课程和计算机技术相结合的一个范例,而它毕竟只是少数学生参加的一项课外科技活动。
数学建模课程和数学建模竞赛的成功和局限性启示我们,开设一门以建立模型和用数学方法及软件求解模型为主要内容的课程是必要的、可能的。
在上述背景下开设数学实验课成为数学教育界的共识:
1995年国家教委启动“高等教育面向21世纪教学内容和课程体系改革”计划,萧树铁先生主持、十余所重点院校参加的“非数学类专业高等数学课程体系和内容改革”项目对课程设置等问题进行了深入研究,在2000年发表的总体构想报告中,明确地把“数学实验”列为非数学类专业的数学基础课。该报告指出:建议开设这门课的目的,是加强学生使用计算机的动手能力与应用意识。 这个以“实验”命名的课程要求以学生自己动手为主,教师的工作主要是介绍必要的数学工具(一般包括数值方法,统计方法和优化方法)、帮助选题、组织讨论和评改作业。一般课堂讲授时间不超过全部学时的一半。与此同时,姜伯驹院士在一篇文章里提出“通过自己动手计算体验解决问题的过程,应该试验组织数学实验课程”。
清华大学数学系参加了上述教改项目,并于1998年在校内进行了数学实验课的试点,姜启源两个学期各开出一次数学实验选修课,在此基础上姜启源等编写了《数学实验》一书(萧树铁教授主编的面向二十一世纪课程教材《大学数学》丛书中的一本,高等教育出版社1999年出版),是国内这门课程(指同类内容)的第一本教材。
最近五、六年来我国不少院校以各种形式将数学实验引入教学,有的作为辅助手段在微积分、线性代数课程中安排软件实习,有的在数学建模课引入数学实验的内容,结合成一门课程,也有的单独设课。
我们充分研究了学生通过数学实验课所应获取的知识和能力,确定了数学实验课的主要内容,又结合目前学校数学教学体系和课程安排,在教学行政部门的支持下,决定将数学实验设定为一门限选课,并从2000年起在我校大规模开课,每学期开3~4个大班(每班约200人),至今已5年半,约7千名学生上过此课。 |